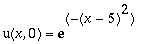
As animações abaixo mostram o movimento de uma corda vibrante com as duas extremidades livres de comprimento L=10 com condições iniciais dadas por:

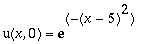
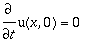
O perfil da corda em t=0 é dado pela figura:

Após o cálculo dos coeficientes de Fourier, conclui-se que os coeficientes ímpares são nulos. A animação abaixo mostra o movimento da corda em tempos posteriores:

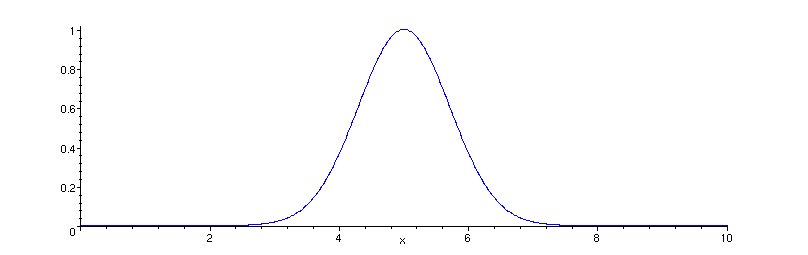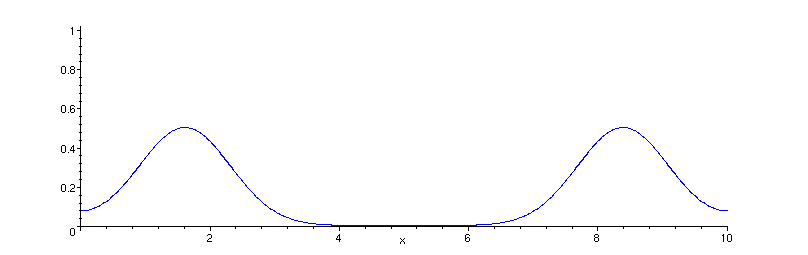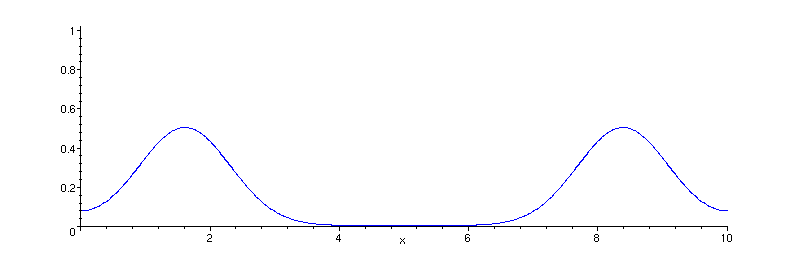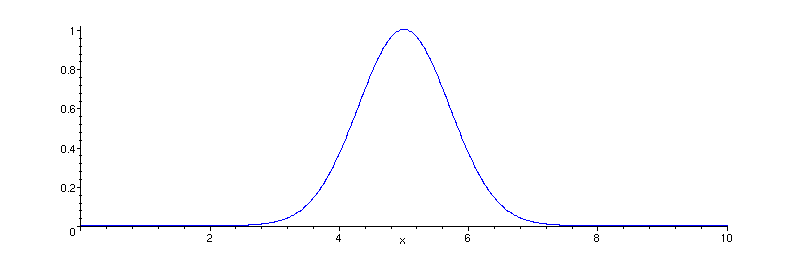
É interessante observar a superposição das ondas, e o fato de que não há inversão da onda nas duas extremidades livres.

A animação abaixo mostra o movimento dos cinco primeiros modos não nulos de oscilação, que são os modos 0, 2, 4, 6 e 8. Note que o primeiro modo é constante, representando o termo a(0) da expansão de Fourier: