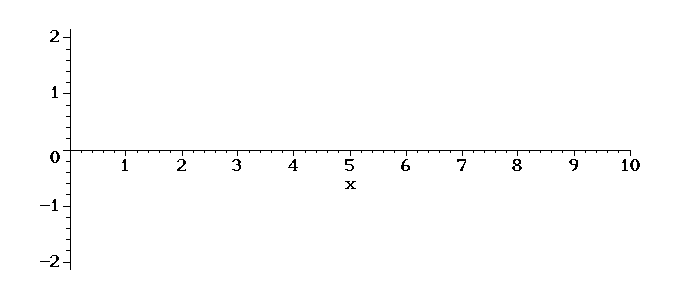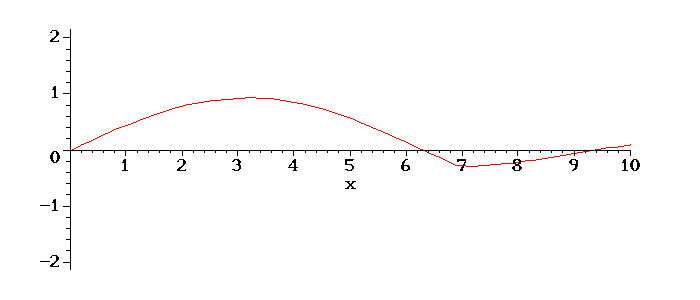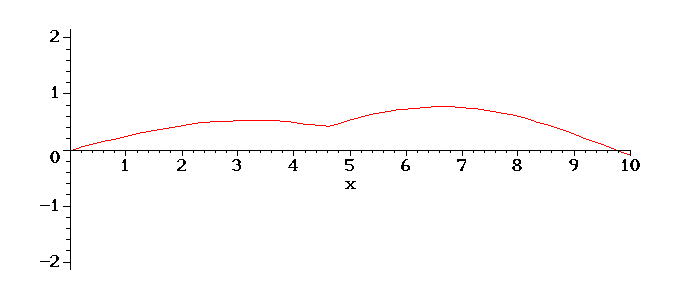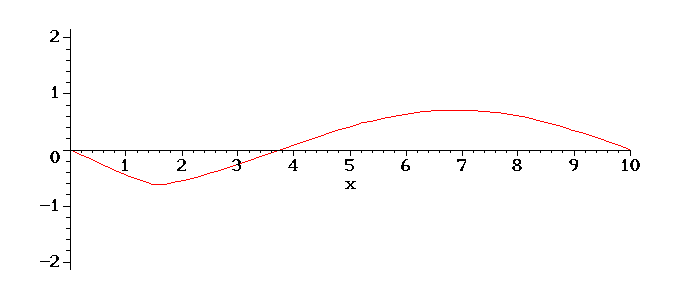Vamos ver como é o movimento de uma corda que é fixa numa extremidade mas que tem um movimento harmônico na outra extremidade. É como se uma pessoa produzisse ondulações numa corda esticada que está presa. A função que descreve o movimento da corda é a equação de onda, dada por:

onde c é a densidade linear de massa da corda. As condições iniciais e de contorno são:

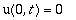
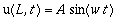
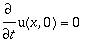
Onde w é a frequência de oscilação na extremidade livre e A a amplitude. De acordo com N. Piskounov - Cálculo Diferencial e Integral, vol.II, a solução geral da equação de onda será, em função dos parâmetros do problema:

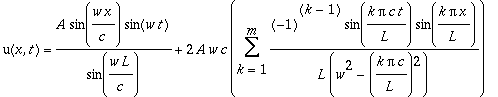
Agora vamos fazer algumas animações com esse resultado, para diversos valores das constantes. O número de termos da expansão m será sempre igual a 100.

Tomando os valores:

L=10,0

w=0,003

c=0,01

A=0,5

Teremos o seguinte movimento da corda em tempos posterios:

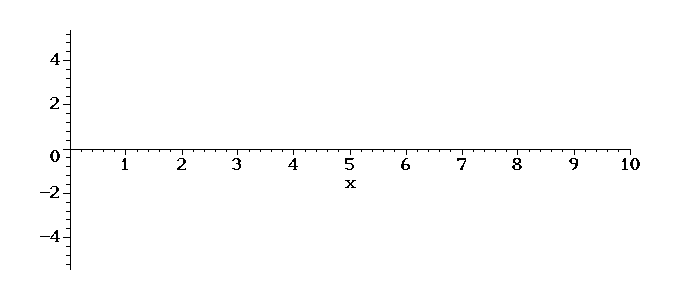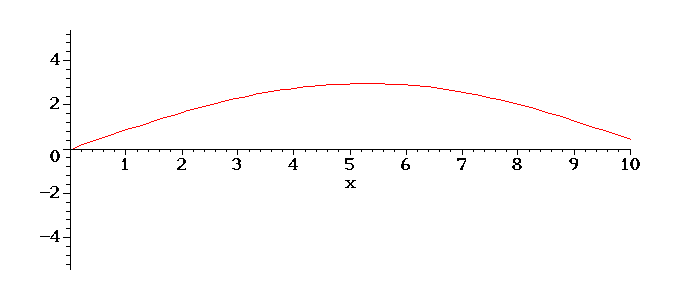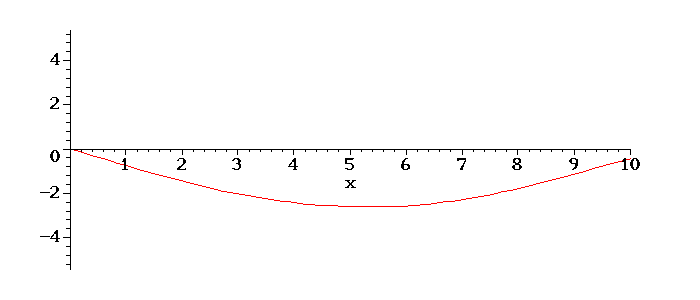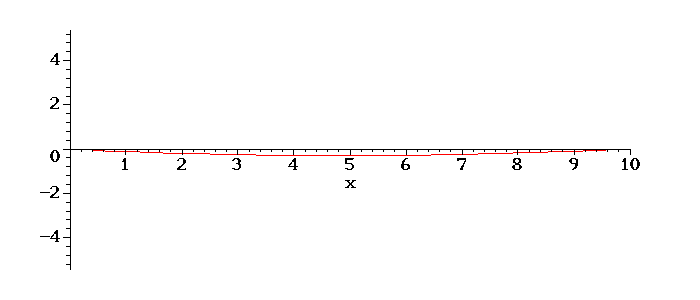
É interessante notar o aumento da amplitude de oscilação, devido ao fato de o valor de w escolhido ser próximo do valor da frequência do primeiro modo de oscilação da corda, ou seja, está próximo de ocorrer uma ressonância, quando a amplitude vai ao infinito.

O mesmo ocorre para w=0,006, onde agora estamos próximo da frequência do segundo modo normal de oscilação.

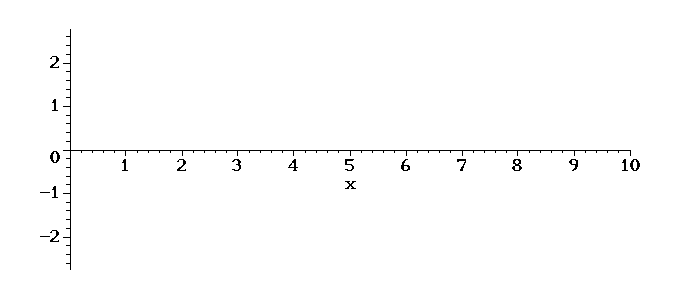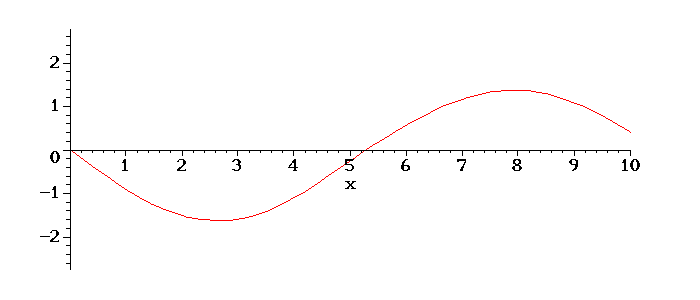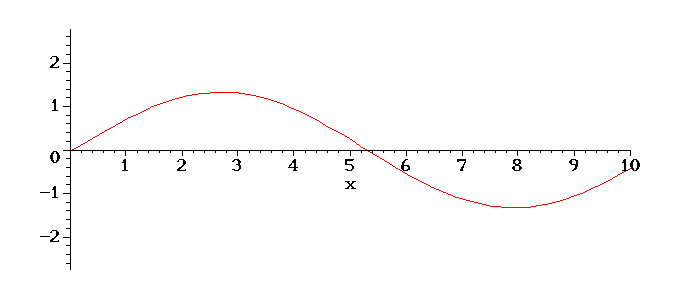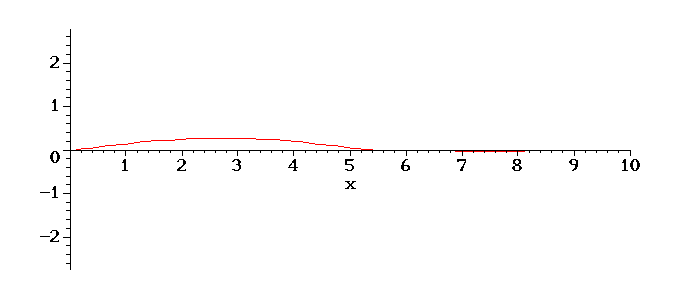
Agora vamos ver a animação para outros valores das constantes. Tomamos os valores:

L=10,0

w=0,0001

c=0,0004

A=1,0

Esses valores representam uma corda de baixa densidade linear de massa e baixa frequência. Teremos o seguinte movimento da corda, onde é interessante observar que, após a reflexão, ocorrem superposições das ondas:

Tomamos agora os valores:

L=10,0

w=0,0001

c=0,02

A=1,0

Esses valores representam uma corda de alta densidade linear de massa, ou seja, uma corda bem esticada, e baixa frequência. Teremos o seguinte movimento da corda, onde é interessante observar que agora não há ondas se propagando, pois o comprimento de onda é maior que o valor de L neste caso:

Se aumentarmos o comprimento da corda, teremos a formação de uma onda. Na animação abaixo usamos os mesmos valores anteriores, no entanto com L=500:

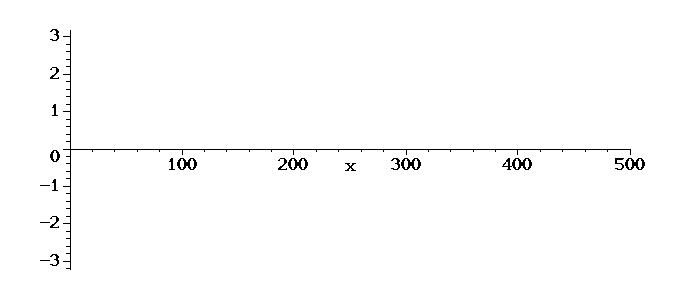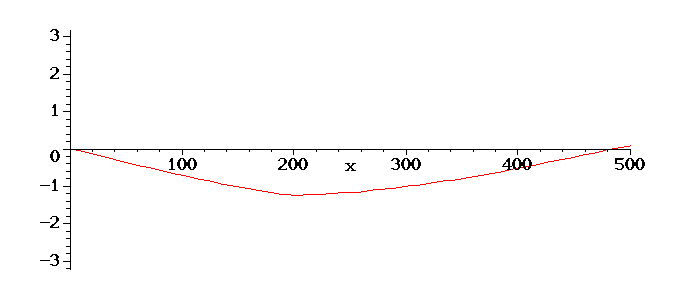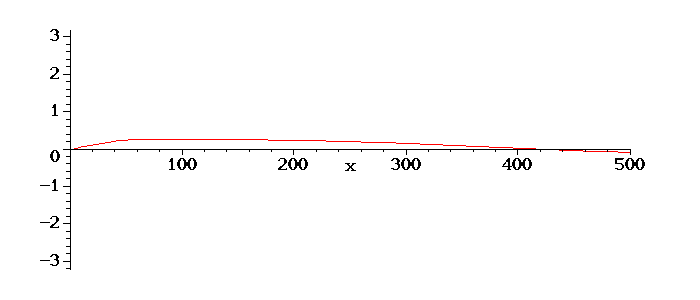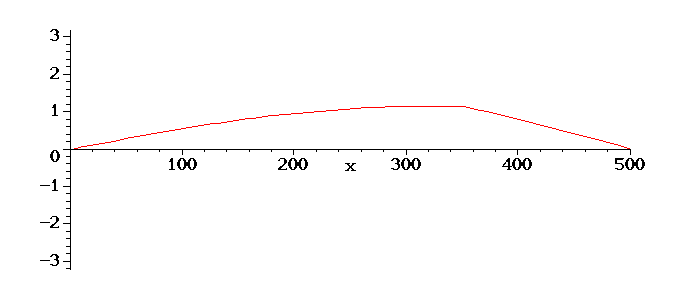
Agora vamos aumentar tanto a frequência quanto a densidade linear de massa:

L=10,0

w=0,4

c=1,0

A=1,0

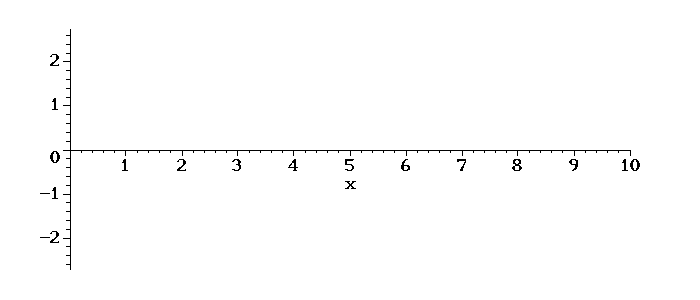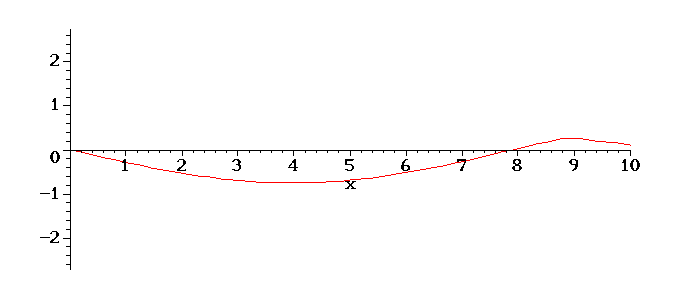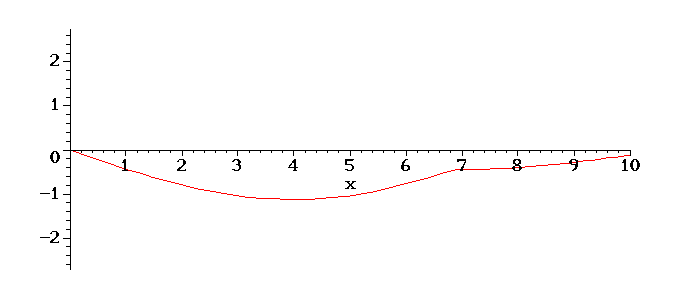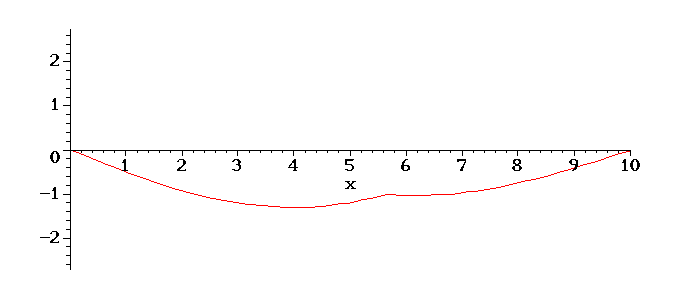
Abaixo mais outro exemplo de condições iniciais:

L=10,0

w=0,001

c=0,002

A=1,0