Fazendo um gráfico de f no intervalo de 0 a 4
.
Animações
que exibem os aproximantes de Fourier de uma função dada
O
que apresentamos abaixo são gráficos e animações referentes à série de
Fourier de uma função tipo dente-de-serra.
Clique aqui
para copiar o programa em Maple V.5 que produziu as animações.
, vale x
no intervalo de 0 a e vale zero no
intervalo de a 2.
Fazendo um gráfico de f no intervalo de 0 a 4.
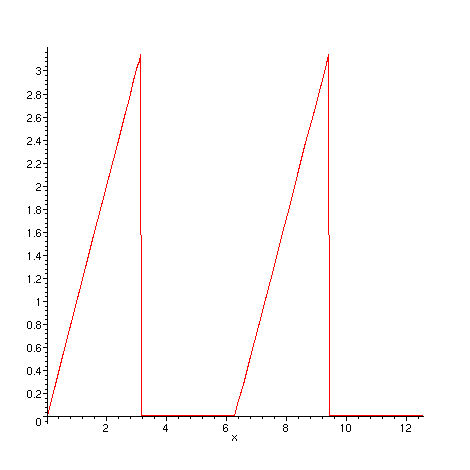
Definindo os coeficientes de Fourier de f:
![[Maple Math]](images/dente_de_serra_12.gif){kind=small}
![[Maple Math]](images/dente_de_serra_13.gif)
![[Maple Math]](images/dente_de_serra_14.gif)
Definindo a função g, que é a aproximação
de ordem N de f, ou seja, a série de Fourier de f calculada até ordem
N.
![[Maple Math]](images/dente_de_serra_15.gif)
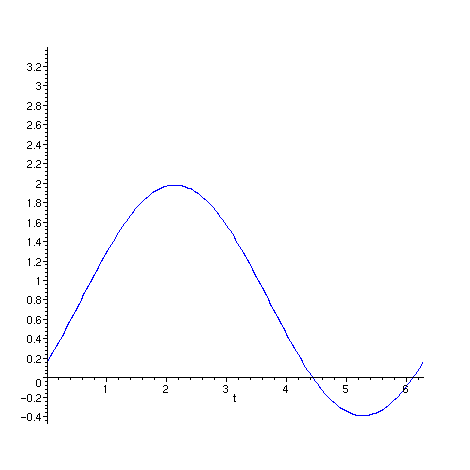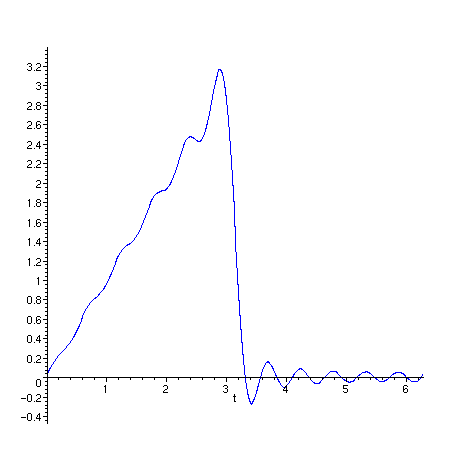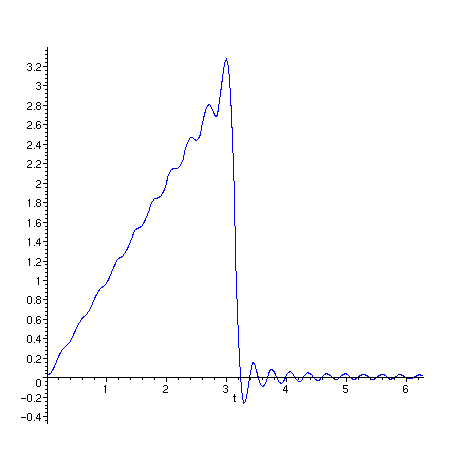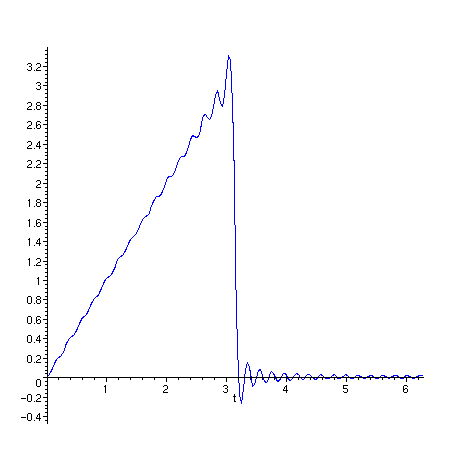
Produzindo uma animação de g para N
variando de 1 a 30 e com x variando de 0 a 2.
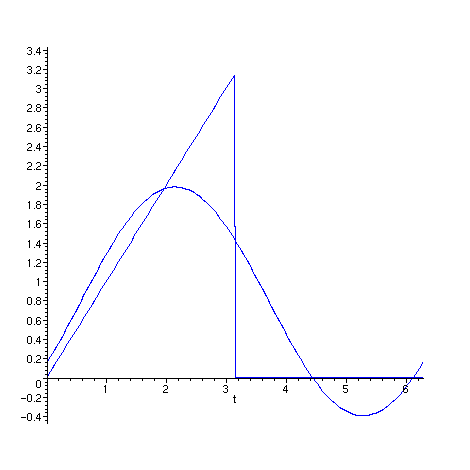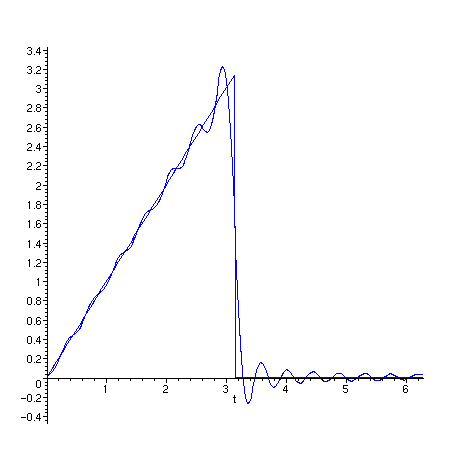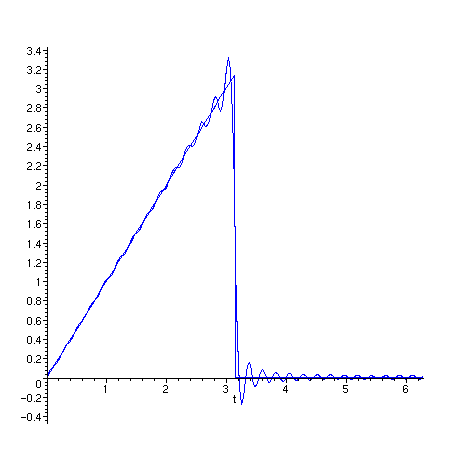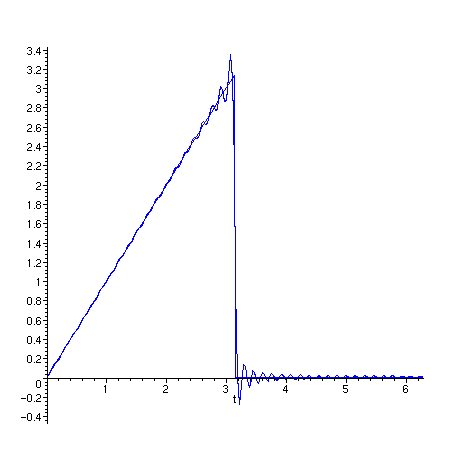
Abaixo mostramos simultaneamente f e
g. Nessa animação N varia de 1 a 40 e x varia de 0 a 2. Repare quão bem g se aproxima de f quando N
cresce.
Novamente uma animação de g com N variando
de 1 a 30. O intervalo de x vai de 0 a 4.
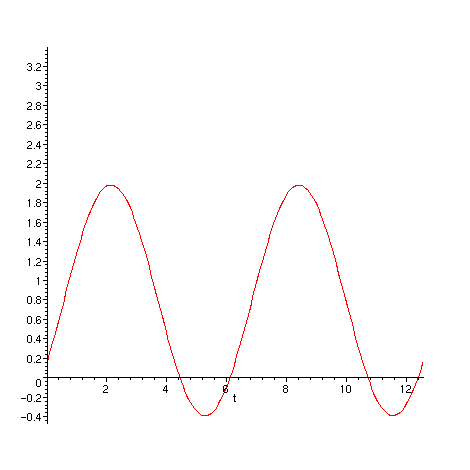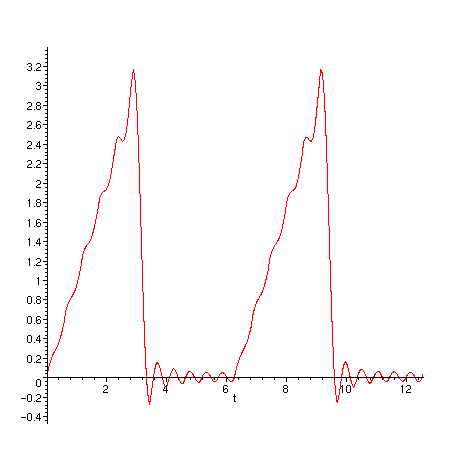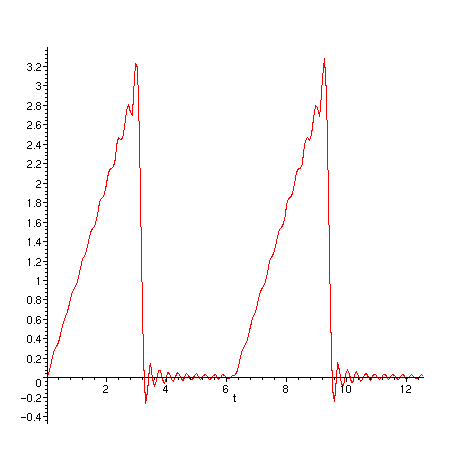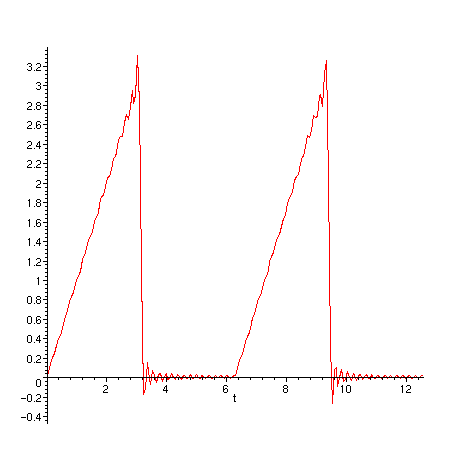
Página do curso de Física-Matemática I