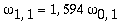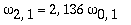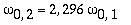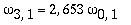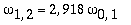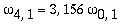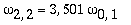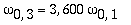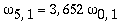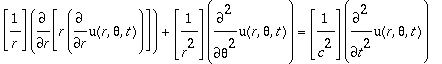
A equação diferencial que descreve o movimento da membrana é, usando coordenadas cilíndricas:

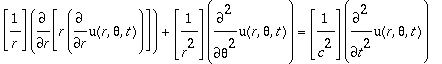
onde r varia de 0 até a e varia de - a , c é a velocidade de propagação das ondas na membrana, e está relacionado com sua densidade de massa.

As condições de contorno são:

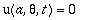
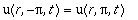
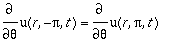
As condições iniciais são:

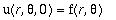
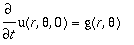
A solução geral será dada por:

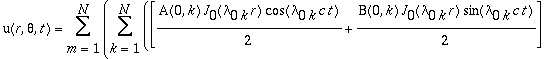
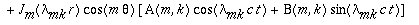
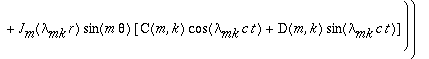
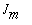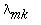Onde representa a m-ésima função de Bessel de primeira ordem e representa o k-ésimo zero da função de Bessel. Os coeficientes A, B, C e D são dados por:

,

,

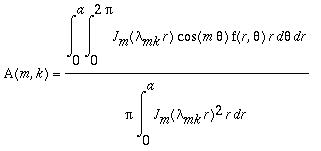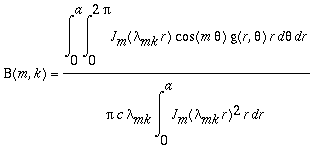
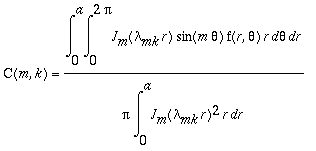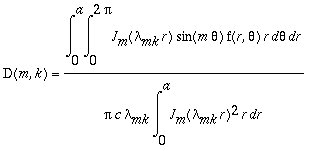
As frequências 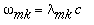são as frequências naturais da membrana e cada membro da soma dupla acima representa um modo natural de vibração. Cada frequência possui dois modos correspondentes, um com cos(m) e o outro com sin(m), exibindo degerescência dupla. As exceções são os casos em que m = 0, representando os modos que possuem simetria radial. Eles são não degenerados. Abaixo mostramos as animações de alguns modos normais.

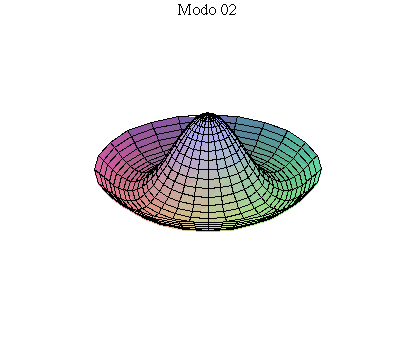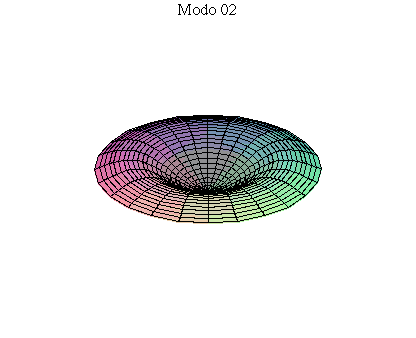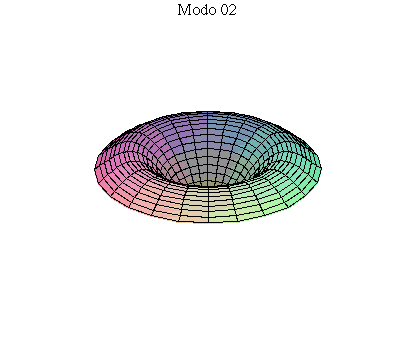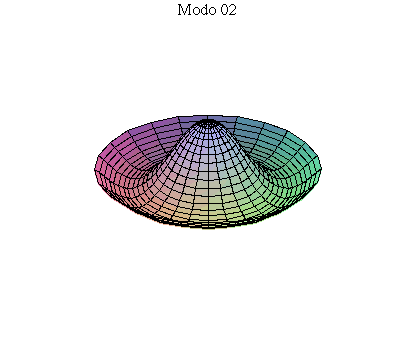
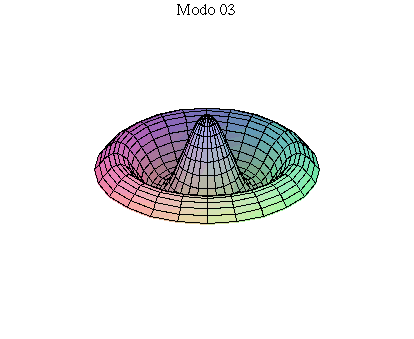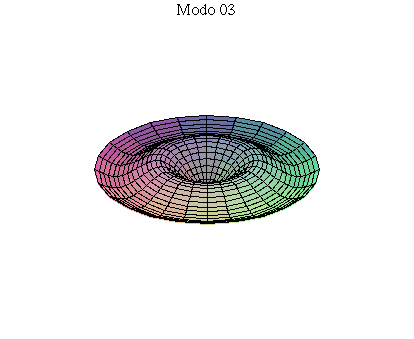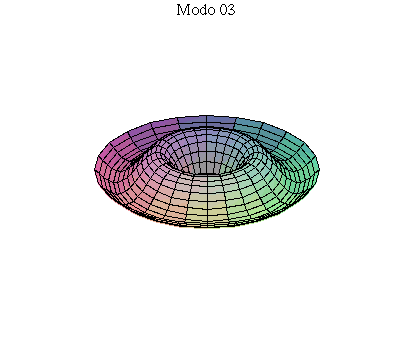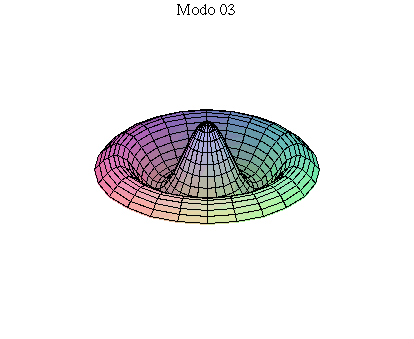
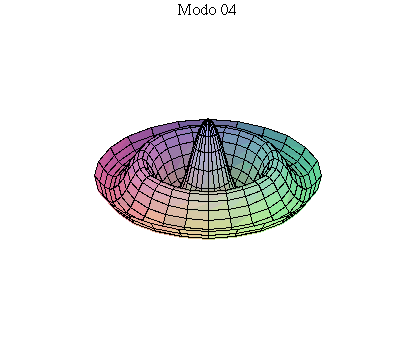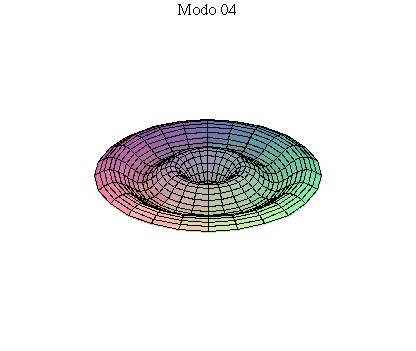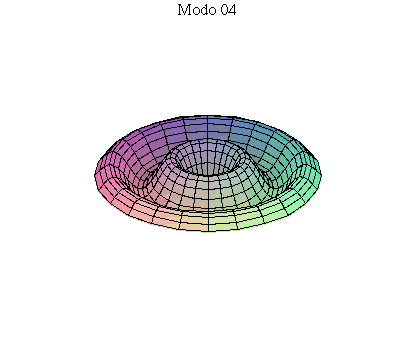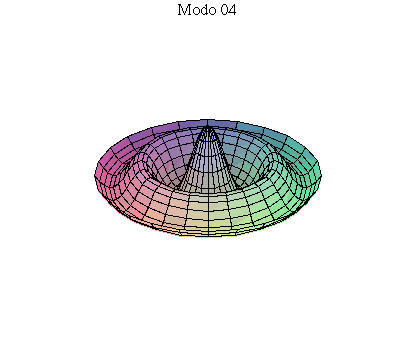
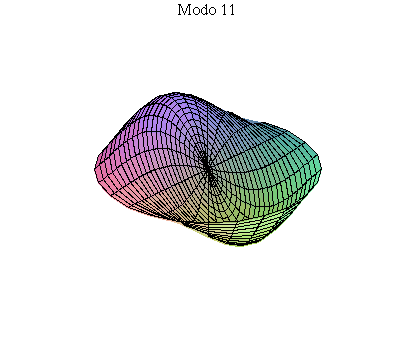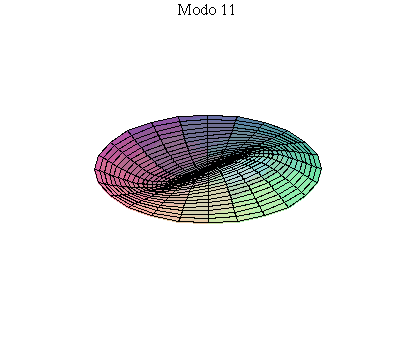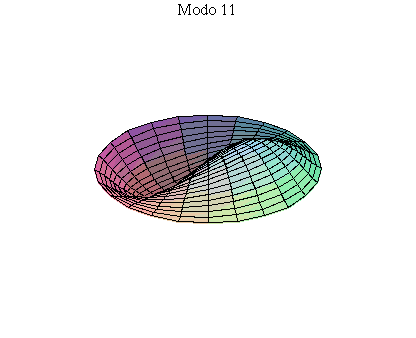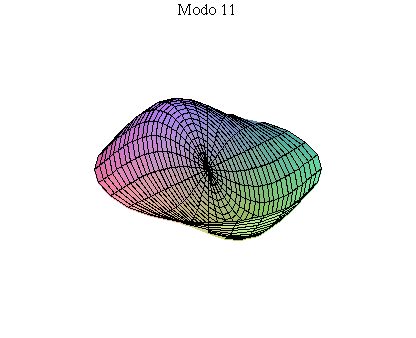
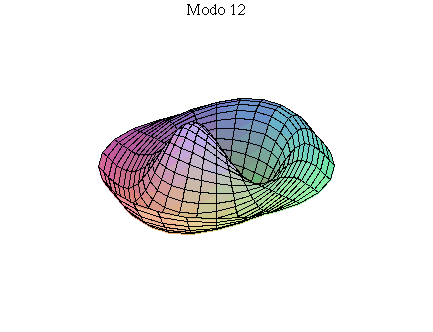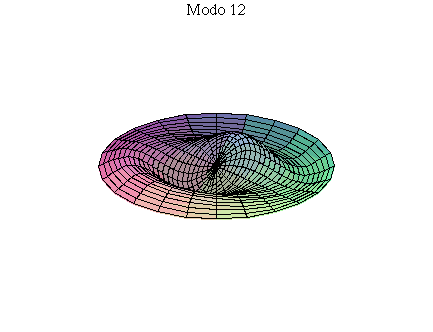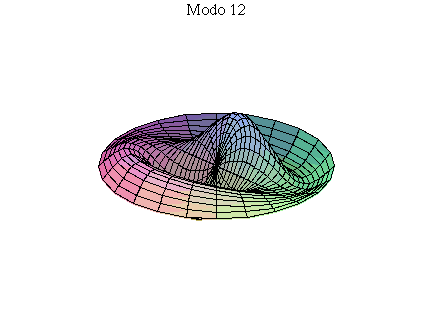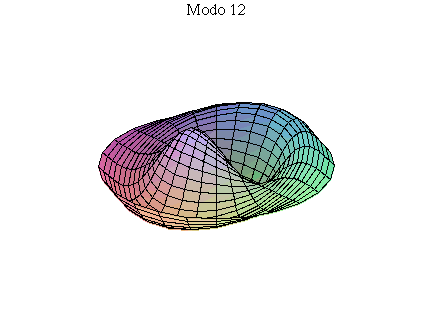
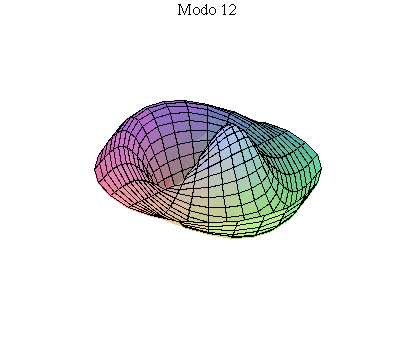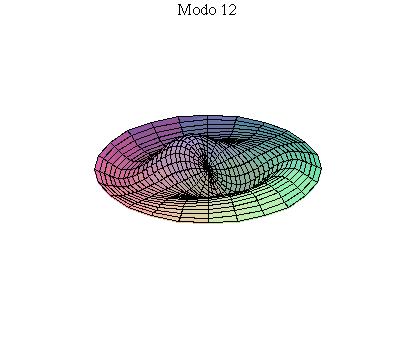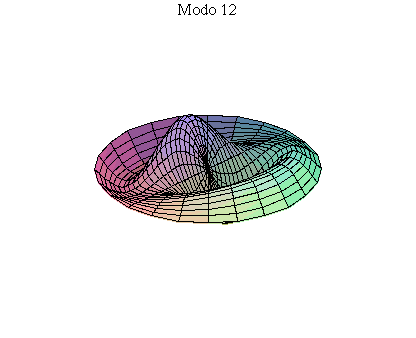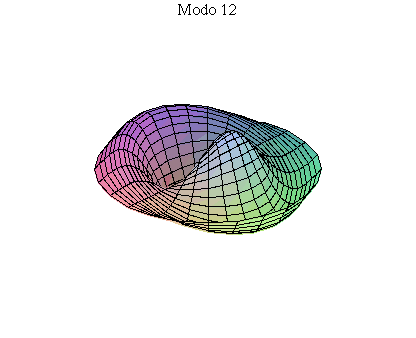
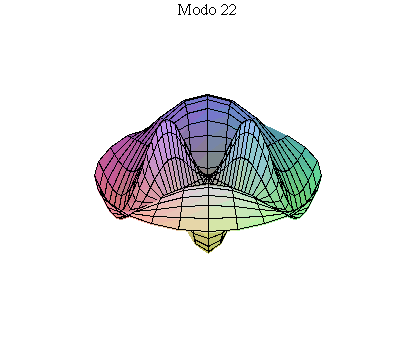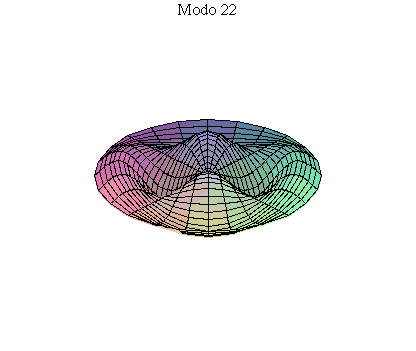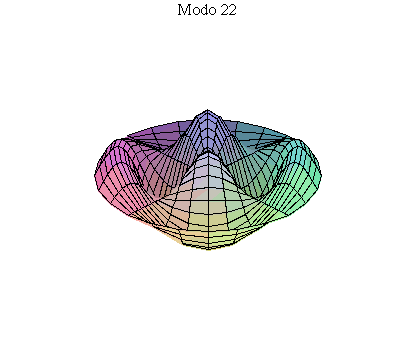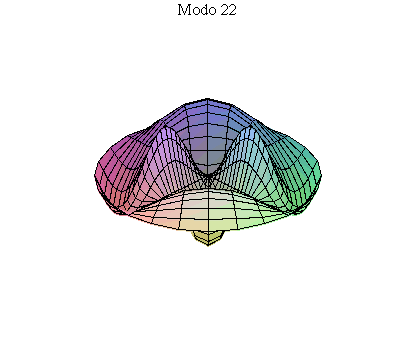
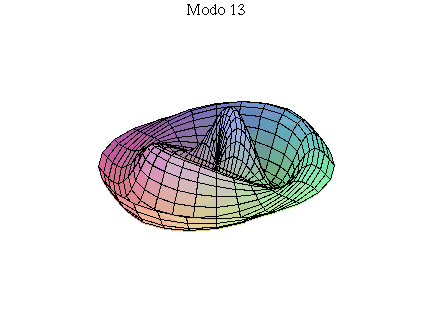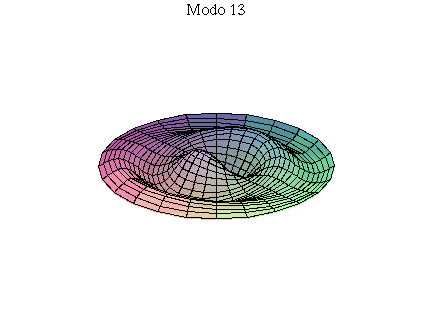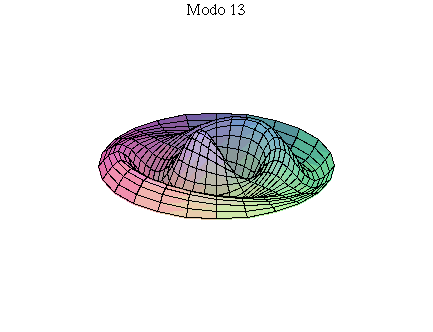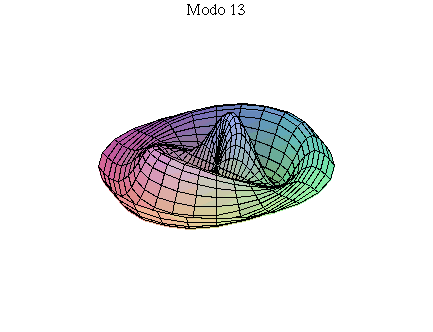
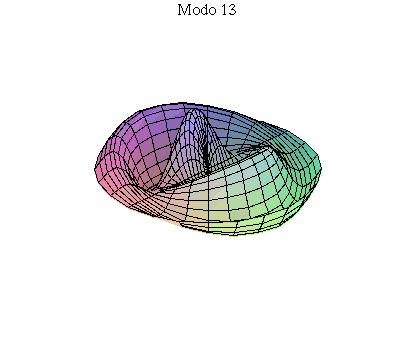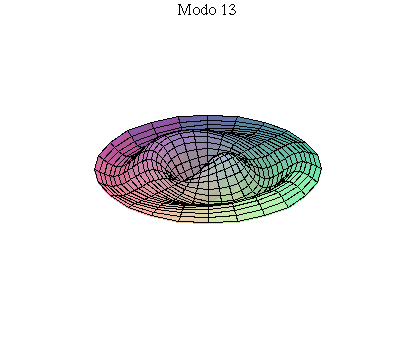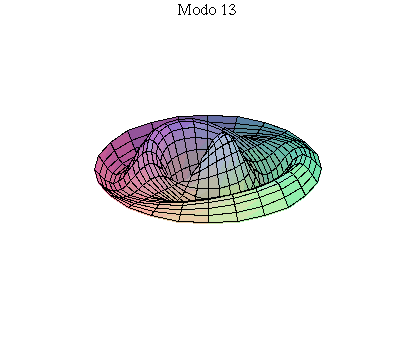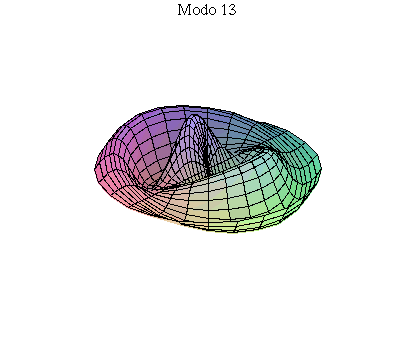
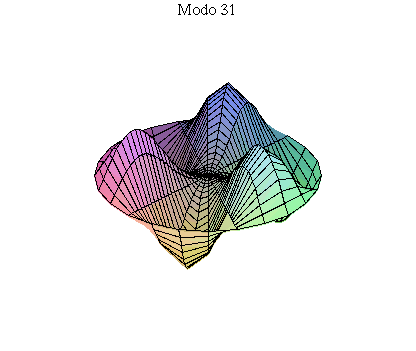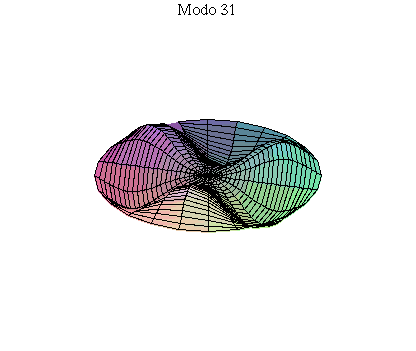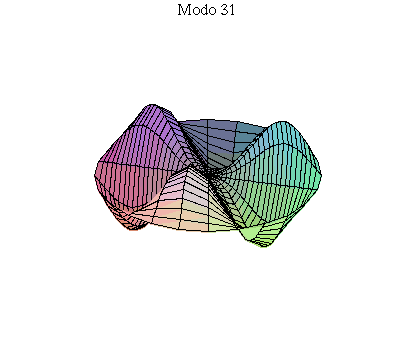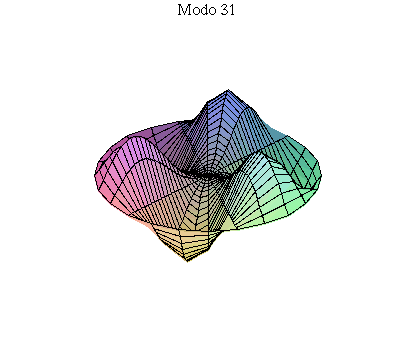
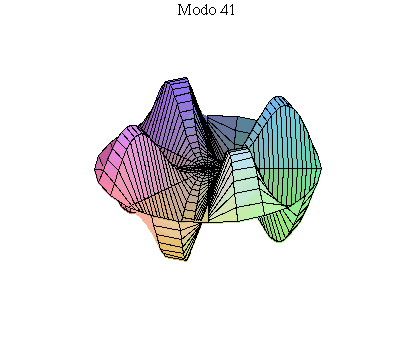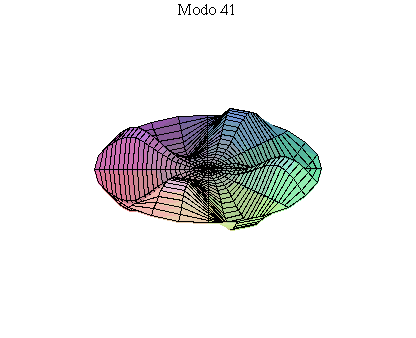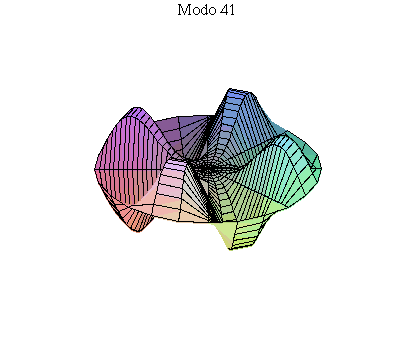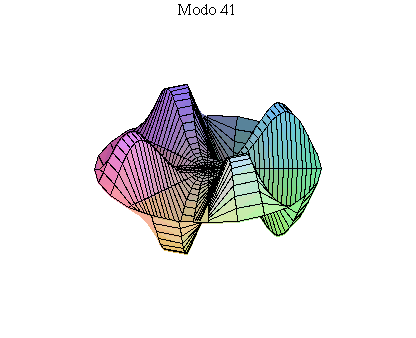
As amplitudes dos modos normais vão depender da função que descreve a posição e velocidade iniciais da membrana. Alguns modos podem estar ausentes na solução final, esses modos não são excitados. As frequências dos modos normais são sempre maiores que a do modo fundamental. Abaixo estão alguns valores em função da frequência fundamental, conforme referência dada acima: