


Next: O Problema da Corda
Up: Funções de Bessel e
Previous: Funções de Bessel e
Funções de Bessel de primeiro tipo e de ordem 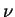 ,
,
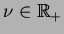 ,
são soluções da seguinte classe de equações diferenciais ordinárias
,
são soluções da seguinte classe de equações diferenciais ordinárias
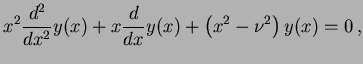 |
(1.1) |
onde
 é uma função a valores reais, contínua e pelo
menos duas vezes diferenciável. A equaçào acima pode ser resolvida
aplicando-se o chamado Método de Frobeniüs. A idéia consiste, essencialmente, em
supormos que a solução de (1.1) seja dada por uma série de
potências com coeficientes a determinar. Assim, escrevemos uma solução
de (1.1) como
é uma função a valores reais, contínua e pelo
menos duas vezes diferenciável. A equaçào acima pode ser resolvida
aplicando-se o chamado Método de Frobeniüs. A idéia consiste, essencialmente, em
supormos que a solução de (1.1) seja dada por uma série de
potências com coeficientes a determinar. Assim, escrevemos uma solução
de (1.1) como
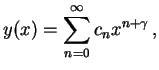 |
(1.2) |
onde
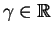 é um parâmetro a mais a ser determinado junto com
o coeficientes
é um parâmetro a mais a ser determinado junto com
o coeficientes
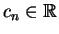 . Como por hipótese (1.2) é solução de
(1.1), fazendo a substituição, obtemos
. Como por hipótese (1.2) é solução de
(1.1), fazendo a substituição, obtemos
Arrumando os termos de forma mais apropriada, temos
Tomando agora 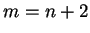 na segunda soma, escrevemos
na segunda soma, escrevemos
Note que as duas somas da última expressão são completamente
independentes. Assim, podemos por 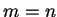 , o que resulta em
, o que resulta em
É conveniente agora escrevermos os dois primeiros termos da primeira
soma explicitamente e deixar o resto dos termos apenas sob um
somatório que vai de 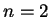 até o infinito. Com efeito,
até o infinito. Com efeito,
Colocando em evidênciando o fator  , para
, para  , temos
, temos
Essa expressão nos diz que a série do lado esquerdo é identicamente
nula. Logo, todos os seus coeficiente devem se anular. Como
conseqüência, valem as seguintes relações para os coeficientes
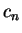 :
:
 |
(1.3) |
![$\displaystyle \left[(1 + \gamma)^2 - \nu^2\right] c_1 = 0 \, ,$](img21.png) |
(1.4) |
 |
(1.5) |
para
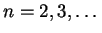 . Observe agora de (1.5) que todos os
coeficientes de índice par maior do que zero (i.e.,
. Observe agora de (1.5) que todos os
coeficientes de índice par maior do que zero (i.e.,
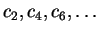 ) são proporcionais à
) são proporcionais à 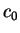 . Da mesma forma, os coeficientes de
índice ímpar são proporcionais à
. Da mesma forma, os coeficientes de
índice ímpar são proporcionais à 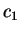 . Portanto, se tentarmos
satisfazer as relações (1.3) e (1.4) fazendo a
escolha ingênua
. Portanto, se tentarmos
satisfazer as relações (1.3) e (1.4) fazendo a
escolha ingênua
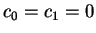 , acabaríamos com
, acabaríamos com 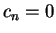 para todo
para todo
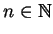 . Obviamente esta é uma solução trivial de
(1.1) a qual não estamos interessados. Por outro
lado, as relações (1.3) e (1.4) podem ser satisfeitas
simultâneamente de duas outras maneiras distintas, sem que acabemos
com a solução trivial. Uma delas é tomar
. Obviamente esta é uma solução trivial de
(1.1) a qual não estamos interessados. Por outro
lado, as relações (1.3) e (1.4) podem ser satisfeitas
simultâneamente de duas outras maneiras distintas, sem que acabemos
com a solução trivial. Uma delas é tomar 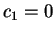 e
e
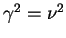 . Outra é
. Outra é  e
e
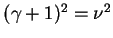 . Não é difícil perceber que quaquer
uma dessas duas escolhas nos leva à verificação das relações (1.3)
e (1.4). Vamos considerar, inicialmente, a primeira opção, ou seja
. Não é difícil perceber que quaquer
uma dessas duas escolhas nos leva à verificação das relações (1.3)
e (1.4). Vamos considerar, inicialmente, a primeira opção, ou seja
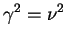 e e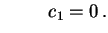 |
(1.6) |
Uma vez que 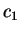 foi escolhido nulo, de acordo com (1.5),
todo coeficiente de índice ímpar também deverá ser nulo, i.e.,
foi escolhido nulo, de acordo com (1.5),
todo coeficiente de índice ímpar também deverá ser nulo, i.e.,
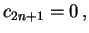 |
(1.7) |
para todo
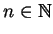 . A condição
. A condição
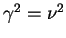 nos dá duas
possibilidades para o valor de
nos dá duas
possibilidades para o valor de 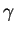 :
:
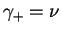 ou
ou
 . No primeiro caso, pela
relação (1.5), teríamos
. No primeiro caso, pela
relação (1.5), teríamos
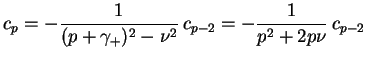 |
(1.8) |
para todo  par,
par,  . Ou seja,
. Ou seja,
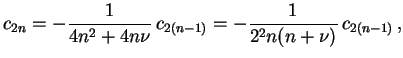 |
(1.9) |
para todo
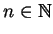 . Por outro lado, quando
. Por outro lado, quando
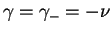 , segue também de (1.5) que
, segue também de (1.5) que
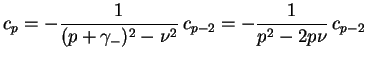 |
(1.10) |
para todo 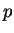 par,
par, 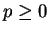 . Quer dizer,
. Quer dizer,
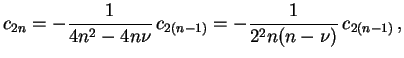 |
(1.11) |
para todo
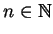 .
.
As expressões (1.9) e (1.11) nos dão, de
forma recursiva, os coeficientes de índice par da expansão
(1.2) sugerida como solução de
(1.1). Lembremos que os coeficientes de índice ímpar são
todos nulos devido à escolha (1.6). Observe agora que como
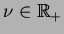 e
e
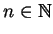 , a expressão
(1.11) é inconveniente quando
, a expressão
(1.11) é inconveniente quando 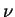 for igual à algum
inteiro positivo. De fato, suponha, por exemplo, que
for igual à algum
inteiro positivo. De fato, suponha, por exemplo, que 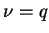 , onde
, onde
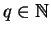 . Então, o coeficente
. Então, o coeficente 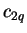 não estaria bem
definido, pois, de acordo com (1.11), teríamos
uma divisão por zero. Isso, entretanto, nunca ocorre com a expressão
(1.9) como pode ser notado claramente. A solução
encontrada para
não estaria bem
definido, pois, de acordo com (1.11), teríamos
uma divisão por zero. Isso, entretanto, nunca ocorre com a expressão
(1.9) como pode ser notado claramente. A solução
encontrada para
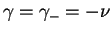 é, portanto, problemática
quando
é, portanto, problemática
quando 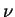 for algum número inteiro positivo. Caso contrário (
for algum número inteiro positivo. Caso contrário (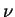 não inteiro), as expressões (1.9) e (1.11)
fornecem duas soluções linearmente independentes da equação (1.1).
não inteiro), as expressões (1.9) e (1.11)
fornecem duas soluções linearmente independentes da equação (1.1).
A solução das equações (1.3), (1.4) e
(1.5) foi obtida mediante a escolha
(1.6). Entretanto, também poderíamos ter escolhido
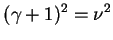 e e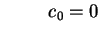 |
(1.12) |
para resolver o problema. Deixamos para o leitor verificar que a
escolha acima leva exatamente à mesma solução que a obtida no caso
anterior. Portanto, as escolhas (1.6) e (1.12) são
equivalentes.
Vamos estudar melhor a solução obtida em (1.9). Note que quando 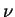 não for um inteiro positivo, os coeficientes em (1.11)
são obtidos dos coeficientes em (1.9) pela substituição
não for um inteiro positivo, os coeficientes em (1.11)
são obtidos dos coeficientes em (1.9) pela substituição
 . Dessa forma, analisaremos apenas a solução
referente aos coeficientes em (1.9). Como
. Dessa forma, analisaremos apenas a solução
referente aos coeficientes em (1.9). Como 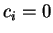 para
todo
para
todo 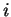 ímpar, uma solução de (1.1) pode ser escrita como
ímpar, uma solução de (1.1) pode ser escrita como
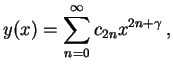 |
(1.13) |
onde, como vimos,
 e
e  é dado por
(1.9), para todo
é dado por
(1.9), para todo
 .
Vamos mostrar por indução em
.
Vamos mostrar por indução em  que
que
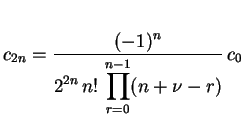 |
(1.14) |
Primeiramente notemos que para  a relação é trivialmente verificada.
De fato, pondo
a relação é trivialmente verificada.
De fato, pondo  em (1.14), temos
em (1.14), temos
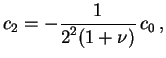 |
(1.15) |
exatamente como em (1.9). Suponha agora, como
hipótese de indução, que
 |
(1.16) |
e vamos mostrar (1.14). Pelas relações (1.9) e
(1.16), segue que
como queríamos demonstrar.
Com a expressão (1.14) em mãos, podemos expressar todos os coeficientes
 de uma forma muito mais elegante, escrevendo-os apenas em
termos do coeficiente
de uma forma muito mais elegante, escrevendo-os apenas em
termos do coeficiente 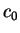 , do parâmetro
, do parâmetro 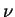 e da ordem
e da ordem  . Com efeito,
. Com efeito,
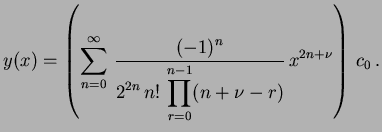 |
(1.17) |
A expressão anterior é uma solução da equação diferencial ordinária de
segunda ordem (1.1). Gostaríamos de frizar que, como
série de potências, a solução acima faz sentido. De fato, o fator
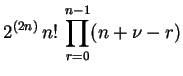 no
denominador dos coeficientes da série faz a mesma convergir
rapidamente (a convergência é uniformemente!) para todos os valores de
no
denominador dos coeficientes da série faz a mesma convergir
rapidamente (a convergência é uniformemente!) para todos os valores de
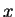 . Note que apenas o termo fatorial no denominador já seria
suficiente para garantir a convergência uniforme da série. Esse é o
caso, por exemplo, da função exponencial
. Note que apenas o termo fatorial no denominador já seria
suficiente para garantir a convergência uniforme da série. Esse é o
caso, por exemplo, da função exponencial
No caso onde 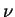 não é um parâmetro inteiro, temos uma outra solução
da equação (1.1) que é obtida de (1.17)
pela substituição
não é um parâmetro inteiro, temos uma outra solução
da equação (1.1) que é obtida de (1.17)
pela substituição
 . Essas duas soluções são
linearmente independentes e constituem uma base à solução geral de
(1.1) (
. Essas duas soluções são
linearmente independentes e constituem uma base à solução geral de
(1.1) (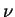 não inteiro!), a qual pode ser escrita como
não inteiro!), a qual pode ser escrita como
onde  e
e 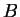 são constantes arbitrárias.
são constantes arbitrárias.
Para terminar esta seção, vamos reescrever a solução
(1.17) de uma forma mais conveniente, de forma que possamos
identificá-la com a chamada função de Bessel de ordem 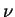 conhecida
da literatura. Lembremos, inicialmente, da definição da função
conhecida
da literatura. Lembremos, inicialmente, da definição da função 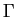 :
:
 |
(1.18) |
Essa função exibe a importante propriedade de que
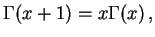 |
(1.19) |
para todo
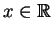 . A demonstração desse fato pode ser feito
mediante uma integração por partes em (1.19). Omitiremos os
detalhes. Observe agora que
. A demonstração desse fato pode ser feito
mediante uma integração por partes em (1.19). Omitiremos os
detalhes. Observe agora que
como conseqüência imediata da propriedade (1.20). Dessa
forma, reescrevemos a solução 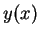 dada em (1.17) como
dada em (1.17) como
 |
(1.20) |
Já que
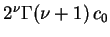 é uma constante (não depende nem
de
é uma constante (não depende nem
de  e nem de
e nem de 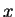 ), podemos expressar
), podemos expressar 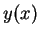 como
como
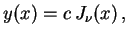 |
(1.21) |
onde 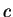 é uma constante e
é uma constante e
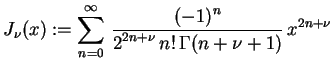 |
(1.22) |
é a camada Função de Bessel de primeiro tipo e ordem
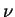 . Portanto, no caso em que
. Portanto, no caso em que 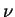 não é um número inteiro
positivo, podemos escrever a solução mais geral da equação
(1.1) como
não é um número inteiro
positivo, podemos escrever a solução mais geral da equação
(1.1) como
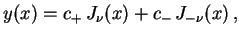 |
(1.23) |
onde 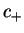 e
e 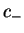 são constantes arbitrárias. Funções de Bessel
de primeiro tipo e ordem
são constantes arbitrárias. Funções de Bessel
de primeiro tipo e ordem 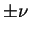 ,
, 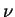 não inteiro, constituem,
portanto, uma base para o espaço de soluções da equação diferencial
(1.1). Por outro lado, quando
não inteiro, constituem,
portanto, uma base para o espaço de soluções da equação diferencial
(1.1). Por outro lado, quando 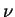 for um inteiro,
temos apenas uma solução bem definida, a saber aquela dada por
(1.22) e (1.23). Uma outra solução,
linearmente independente a essa, envolve uma função não-analítica em torno
da origem (singular) a qual não pode ser expressa em forma de uma
série de potências como em (1.2). Essa solução singular (no
caso
for um inteiro,
temos apenas uma solução bem definida, a saber aquela dada por
(1.22) e (1.23). Uma outra solução,
linearmente independente a essa, envolve uma função não-analítica em torno
da origem (singular) a qual não pode ser expressa em forma de uma
série de potências como em (1.2). Essa solução singular (no
caso 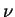 inteiro) é conhecida como função de Bessel de segundo tipo
e ordem
inteiro) é conhecida como função de Bessel de segundo tipo
e ordem 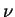 , ou função de Neuman de ordem
, ou função de Neuman de ordem 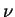 .
.
Estaremos, a seguir, estudando uma aplicação simples em física na qual nos
deparamos com o problema de resolver uma equação diferencial do tipo da
(1.1). Para isso, escreveremos nossa solução em termos
das funções de Bessel introduzidas aqui.



Next: O Problema da Corda
Up: Funções de Bessel e
Previous: Funções de Bessel e
Daniel Augusto Cortez
2002-07-12
![]() ,
,
![]() ,
são soluções da seguinte classe de equações diferenciais ordinárias
,
são soluções da seguinte classe de equações diferenciais ordinárias
![\begin{multline}
x^2 \left[\sum_{n=0}^{\infty }(n+\gamma)(n+\gamma-1)c_n
x^{n+\g...
...t[\sum_{n=0}^{\infty } c_n
x^{n+\gamma}\right] = 0 \, . \nonumber
\end{multline}](img8.png)
![$\displaystyle \sum_{n=0}^{\infty } \left[(n+\gamma)^2 - \nu^2 \right] c_n x^{n+\gamma} + \sum_{n=0}^{\infty } c_n x^{n+\gamma+2} = 0 \, ,$](img9.png)
![$\displaystyle \sum_{n=0}^{\infty } \left[(n+\gamma)^2 - \nu^2 \right] c_n x^{n+\gamma} + \sum_{m=2}^{\infty } c_{m-2} x^{m+\gamma} = 0 \, .$](img11.png)
![$\displaystyle \sum_{n=0}^{\infty } \left[(n+\gamma)^2 - \nu^2 \right] c_n x^{n+\gamma} + \sum_{n=2}^{\infty } c_{n-2} x^{n+\gamma} = 0 \, .$](img13.png)
![$\displaystyle \left(\gamma^2-\nu^2\right) c_0 x^\gamma + \left[(1+\gamma)^2 - \...
...{ \left[(n+\gamma)^2 - \nu^2\right] c_n + c_{n-2}\right\} x^{n+\gamma} = 0 \, .$](img15.png)
![$\displaystyle \left(\gamma^2-\nu^2\right) c_0 + \left[(1+\gamma)^2 - \nu^2\righ...
... \left\{ \left[(n+\gamma)^2 - \nu^2\right] c_n + c_{n-2}\right\} x^{n} = 0 \, .$](img18.png)
![]() e
e
![]() , a expressão
(1.11) é inconveniente quando
, a expressão
(1.11) é inconveniente quando ![]() for igual à algum
inteiro positivo. De fato, suponha, por exemplo, que
for igual à algum
inteiro positivo. De fato, suponha, por exemplo, que ![]() , onde
, onde
![]() . Então, o coeficente
. Então, o coeficente ![]() não estaria bem
definido, pois, de acordo com (1.11), teríamos
uma divisão por zero. Isso, entretanto, nunca ocorre com a expressão
(1.9) como pode ser notado claramente. A solução
encontrada para
não estaria bem
definido, pois, de acordo com (1.11), teríamos
uma divisão por zero. Isso, entretanto, nunca ocorre com a expressão
(1.9) como pode ser notado claramente. A solução
encontrada para
![]() é, portanto, problemática
quando
é, portanto, problemática
quando ![]() for algum número inteiro positivo. Caso contrário (
for algum número inteiro positivo. Caso contrário (![]() não inteiro), as expressões (1.9) e (1.11)
fornecem duas soluções linearmente independentes da equação (1.1).
não inteiro), as expressões (1.9) e (1.11)
fornecem duas soluções linearmente independentes da equação (1.1).
![]() não for um inteiro positivo, os coeficientes em (1.11)
são obtidos dos coeficientes em (1.9) pela substituição
não for um inteiro positivo, os coeficientes em (1.11)
são obtidos dos coeficientes em (1.9) pela substituição
![]() . Dessa forma, analisaremos apenas a solução
referente aos coeficientes em (1.9). Como
. Dessa forma, analisaremos apenas a solução
referente aos coeficientes em (1.9). Como ![]() para
todo
para
todo ![]() ímpar, uma solução de (1.1) pode ser escrita como
ímpar, uma solução de (1.1) pode ser escrita como
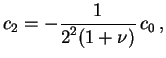

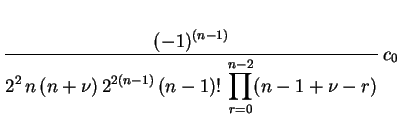
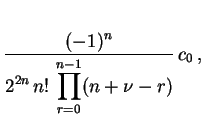
![]() de uma forma muito mais elegante, escrevendo-os apenas em
termos do coeficiente
de uma forma muito mais elegante, escrevendo-os apenas em
termos do coeficiente ![]() , do parâmetro
, do parâmetro ![]() e da ordem
e da ordem ![]() . Com efeito,
. Com efeito,
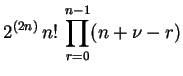 no
denominador dos coeficientes da série faz a mesma convergir
rapidamente (a convergência é uniformemente!) para todos os valores de
no
denominador dos coeficientes da série faz a mesma convergir
rapidamente (a convergência é uniformemente!) para todos os valores de
![]() . Note que apenas o termo fatorial no denominador já seria
suficiente para garantir a convergência uniforme da série. Esse é o
caso, por exemplo, da função exponencial
. Note que apenas o termo fatorial no denominador já seria
suficiente para garantir a convergência uniforme da série. Esse é o
caso, por exemplo, da função exponencial
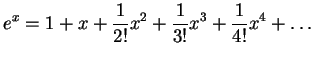
![]() não é um parâmetro inteiro, temos uma outra solução
da equação (1.1) que é obtida de (1.17)
pela substituição
não é um parâmetro inteiro, temos uma outra solução
da equação (1.1) que é obtida de (1.17)
pela substituição
![]() . Essas duas soluções são
linearmente independentes e constituem uma base à solução geral de
(1.1) (
. Essas duas soluções são
linearmente independentes e constituem uma base à solução geral de
(1.1) (![]() não inteiro!), a qual pode ser escrita como
não inteiro!), a qual pode ser escrita como
![]() conhecida
da literatura. Lembremos, inicialmente, da definição da função
conhecida
da literatura. Lembremos, inicialmente, da definição da função ![]() :
:
![$\displaystyle \Gamma(n+\nu+1) = (n+\nu)\Gamma(n+\nu) = \left[\prod_{r=0}^{n-1} (n+\nu -m)\right] \, \Gamma(\nu + 1) \, ,$](img78.png)