


Next: About this document ...
Up: Funções de Bessel e
Previous: Introdução. Funções de Bessel
Considere uma corda de seção tranversal constante e densidade linear
de massa igual à  , também constante. Suponha que essa corda
tenha comprimento
, também constante. Suponha que essa corda
tenha comprimento  e que uma das extremidades da mesma esteja fixada em
um dado ponto do espaço. A corda assim descrita estará sujeita a ação de
seu próprio peso devido à aceleração da gravidade local.
Suponha conhecida a posição e a velocidade de todos os pontos da corda em
um dado instante de tempo inicial
e que uma das extremidades da mesma esteja fixada em
um dado ponto do espaço. A corda assim descrita estará sujeita a ação de
seu próprio peso devido à aceleração da gravidade local.
Suponha conhecida a posição e a velocidade de todos os pontos da corda em
um dado instante de tempo inicial 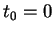 . Nessas condições, gostaríamos
de descrever o movimento da corda para
. Nessas condições, gostaríamos
de descrever o movimento da corda para  . Como veremos a seguir,
esse é um problema cuja solução envolve as funções de Bessel discutidas
anteriormente.
. Como veremos a seguir,
esse é um problema cuja solução envolve as funções de Bessel discutidas
anteriormente.
O problema da corda pendurada pode ser colocado de forma matematicamente
precisa da seguinte forma: Seja 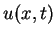 a função que descreve o perfil da
corda no instante de tempo
a função que descreve o perfil da
corda no instante de tempo 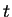 , ou seja,
, ou seja, 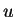 dá o deslocamento do ponto
dá o deslocamento do ponto 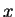 da corda no instante
da corda no instante 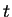 . Suponha que a corda esteja presa em
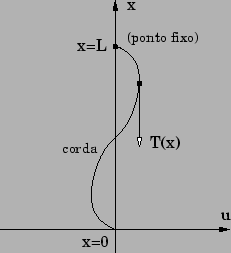
. Suponha que a corda esteja presa em  (vide
figura 1). Nesse caso, devemos impor a seguinte consdição
sob a função
(vide
figura 1). Nesse caso, devemos impor a seguinte consdição
sob a função 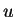 :
:
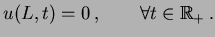 |
(2.1) |
A outra extremidade da corda (o ponto 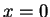 ) está livre para oscilar.
Conseqüêntemente, é razoável impormos que o deslocamento
) está livre para oscilar.
Conseqüêntemente, é razoável impormos que o deslocamento 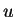 da corda
nesse ponto seja finito, isto é
da corda
nesse ponto seja finito, isto é
 |
(2.2) |
As relações (2.1) e (2.2) escritas acima prescrevem
as chamadas condições de contorno do problema da corda pendurada.
Figura:
Desenho esquemático da corda pendurada.
 |
Conforme já havíamos mencionado, vamos também supor conhecidas a posição e
a velocidade inicial de todos os pontos da corda, ou seja, são nos dadas
funções 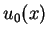 e
e 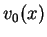 tais que
tais que
![$\displaystyle u(x, 0) = u_0(x) \, , \qquad \forall x \in [0, L]$](img103.png) |
(2.3) |
e
![$\displaystyle \frac{\partial u}{\partial t} (x, 0) = v_0(x) \, , \qquad \forall x \in [0, L] \, .$](img104.png) |
(2.4) |
Essas são as condições iniciais do problema.
Como é bem sabido, o movimento de uma corda vibrante, do tipo considerada
aqui, é regido pela seguinte equação diferencial parcial:
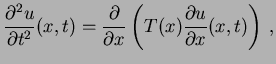 |
(2.5) |
onde 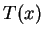 representa a força de tração aplicada na corda sob o seu
ponto de coordenada
representa a força de tração aplicada na corda sob o seu
ponto de coordenada 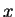 (confira figura 1).
A única força que age sobre a corda pendurada é o seu peso, logo
(confira figura 1).
A única força que age sobre a corda pendurada é o seu peso, logo
sendo 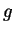 a aceleração da gravidade. Substituindo
a aceleração da gravidade. Substituindo 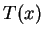 em (2.5), temos
em (2.5), temos
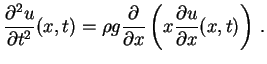 |
(2.6) |
A equação diferencia parcial acima pode ser facilmente resolvida pelo
método de separação de variáveis. Assim, ecrevendo
resulta que
onde o ponto denota derivada temporal e a linha derivada espacial. Como o
lado esquerdo da última relação só depende do tempo e o lado direito só
depende da posição, ambos devem ser necessariamente iguais a uma
constante. Como veremos, essa constante deve ser negativa. Assim,
onde 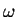 é uma constante real. A equação para a parte temporal fica
é uma constante real. A equação para a parte temporal fica
cuja bem conhecida solução é
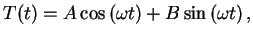 |
(2.7) |
onde  e
e 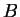 são duas constantes arbitrárias.
Vale a pena observar que se a constante de separação de variáveis
são duas constantes arbitrárias.
Vale a pena observar que se a constante de separação de variáveis
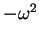 fosse positiva, isto é,
fosse positiva, isto é, 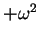 , então a solução para
, então a solução para
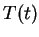 seria exponencialmente crescente ou decrescente, violando a
conservação de energia mecânica da corda.
seria exponencialmente crescente ou decrescente, violando a
conservação de energia mecânica da corda.
Vamos agora nos concentrar em resolver a parte espacial. A equação para
 pode ser escrita como
pode ser escrita como
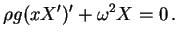 |
(2.8) |
e deve ser tal que
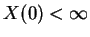 e
e 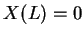 devido às condições de
contorno. Fazendo a mudança de variável
devido às condições de
contorno. Fazendo a mudança de variável
podemos reescrever (2.8) como
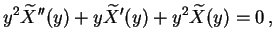 |
(2.9) |
onde
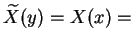 e a linha agora denota derivação com relação à
e a linha agora denota derivação com relação à
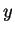 . A equação diferencial (2.9) é idêntica à
(1.1) para
. A equação diferencial (2.9) é idêntica à
(1.1) para 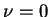 . Como sabemos, a solução de tal equação
é composta pela função de Bessel de ordem zero
. Como sabemos, a solução de tal equação
é composta pela função de Bessel de ordem zero  e uma função de
Neuman que é singular na origem (note que
e uma função de
Neuman que é singular na origem (note que 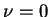 corresponde a um caso
onde
corresponde a um caso
onde 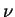 é inteiro). Entretanto, devido à condição de contorno
é inteiro). Entretanto, devido à condição de contorno
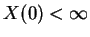 , devemos excluir essa função singular da solução do
problema. Portanto,
, devemos excluir essa função singular da solução do
problema. Portanto,
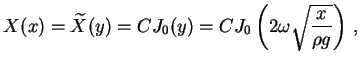 |
(2.10) |
onde 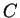 é uma constante arbitrária. Resta ainda impormos à solução acima a
condição de contorno de extremo fixo
é uma constante arbitrária. Resta ainda impormos à solução acima a
condição de contorno de extremo fixo 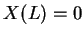 . Essa condição impoem
restrições sobre os valores de
. Essa condição impoem
restrições sobre os valores de  . De fato,
. De fato,
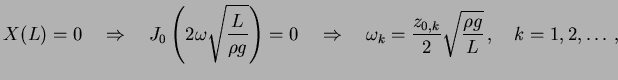 |
(2.11) |
onde 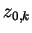 representa o
representa o 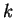 -ésimo zero positivo de
-ésimo zero positivo de  . Os
diferentes modos de vibração da corda são descritos pelas freqüências
. Os
diferentes modos de vibração da corda são descritos pelas freqüências
 . O movimento da corda no
. O movimento da corda no 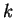 -ésimo modo de vibração é dado por
(2.7) e (2.10) com
-ésimo modo de vibração é dado por
(2.7) e (2.10) com 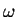 substituido por
substituido por  como
em (2.11). Assim,
como
em (2.11). Assim,
onde 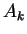 e
e 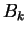 são constantes arbitrárias. O movimento mais geral da
corda é obtido pela superposição de seus modos normais de vibração. Assim,
a solução mais geral da equação (2.6) com as condições de
contorno estabelecidas é
são constantes arbitrárias. O movimento mais geral da
corda é obtido pela superposição de seus modos normais de vibração. Assim,
a solução mais geral da equação (2.6) com as condições de
contorno estabelecidas é
![$\displaystyle u(x, t) = \sum_{k = 1}^{\infty} J_0\left(z_{0, k} \sqrt{\frac{x}{...
..._k \sin \left( \frac{z_{0, k}}{2}\sqrt{\frac{\rho g}{L}} t \right) \right] \, .$](img139.png) |
(2.12) |
Note que a corda descreve um movimento quase-periódico no
tempo. Entretanto, cada modo normal isoladamente tem um período bem
definido, a saber
Resta agora impormos as condições iniciais (2.3) e (2.4)
à solução (2.12). Isso pode ser feito usando a seguinte
relação de ortogonalidade entre as funções de Bessel:
onde 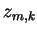 é o
é o 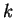 -ésimo zero da função de Bessel
-ésimo zero da função de Bessel 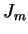 . Fazendo
. Fazendo
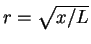 na integral acima e especializando para
na integral acima e especializando para  , temos
, temos
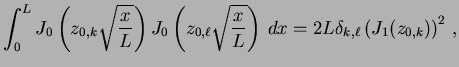 |
(2.13) |
No instante de tempo 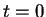 ,
, 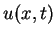 em (2.12) se
reduz à
em (2.12) se
reduz à
que, de acordo com (2.3), deve ser igual à 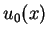 . Multiplicando
ambos os lados por
. Multiplicando
ambos os lados por
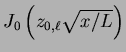 ,
integrando em
,
integrando em 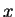 de 0 à
de 0 à  e usando a relação de ortogonalidade
(2.13), achamos
e usando a relação de ortogonalidade
(2.13), achamos
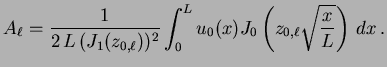 |
(2.14) |
Essa expressão fixa o valor de todas as constantes 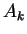 em
(2.12) para que a condição inicial
em
(2.12) para que a condição inicial
 seja
satisfeita. Devemos ainda fixar as constantes
seja
satisfeita. Devemos ainda fixar as constantes 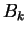 . Isso é feito a partir
da outra condição inicial, isto é, (2.4). Primeiramente, derivamos
. Isso é feito a partir
da outra condição inicial, isto é, (2.4). Primeiramente, derivamos
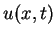 com relação ao tempo:
com relação ao tempo:
Para 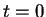 , temos
, temos
Usando, novamente, a relação de ortogonalidade (2.13), podemos
inverter a relação acima e escrever cada constante  como
como
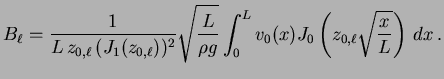 |
(2.15) |
A solução final da equação (2.6) satisfazendo tanto as condições
de contorno quanto as condições iniciais é finalmente obtida substituindo
os coeficientes  e
e  obtidos em (2.14) e
(2.15) na expressão (2.12) para
obtidos em (2.14) e
(2.15) na expressão (2.12) para 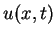 . Com
efeito, trocando a ordem da soma com a integral, podemos escrever
. Com
efeito, trocando a ordem da soma com a integral, podemos escrever
que é o resultado desejado.



Next: About this document ...
Up: Funções de Bessel e
Previous: Introdução. Funções de Bessel
Daniel Augusto Cortez
2002-07-12
![]() , também constante. Suponha que essa corda
tenha comprimento
, também constante. Suponha que essa corda
tenha comprimento ![]() e que uma das extremidades da mesma esteja fixada em
um dado ponto do espaço. A corda assim descrita estará sujeita a ação de
seu próprio peso devido à aceleração da gravidade local.
Suponha conhecida a posição e a velocidade de todos os pontos da corda em
um dado instante de tempo inicial
e que uma das extremidades da mesma esteja fixada em
um dado ponto do espaço. A corda assim descrita estará sujeita a ação de
seu próprio peso devido à aceleração da gravidade local.
Suponha conhecida a posição e a velocidade de todos os pontos da corda em
um dado instante de tempo inicial ![]() . Nessas condições, gostaríamos
de descrever o movimento da corda para
. Nessas condições, gostaríamos
de descrever o movimento da corda para ![]() . Como veremos a seguir,
esse é um problema cuja solução envolve as funções de Bessel discutidas
anteriormente.
. Como veremos a seguir,
esse é um problema cuja solução envolve as funções de Bessel discutidas
anteriormente.
![]() a função que descreve o perfil da
corda no instante de tempo
a função que descreve o perfil da
corda no instante de tempo ![]() , ou seja,
, ou seja, ![]() dá o deslocamento do ponto
dá o deslocamento do ponto ![]() da corda no instante
da corda no instante ![]() . Suponha que a corda esteja presa em
. Suponha que a corda esteja presa em ![]() (vide
figura 1). Nesse caso, devemos impor a seguinte consdição
sob a função
(vide
figura 1). Nesse caso, devemos impor a seguinte consdição
sob a função ![]() :
:
![]() e
e ![]() tais que
tais que
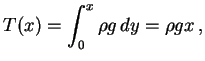
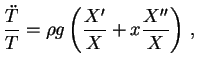
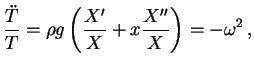
![]() pode ser escrita como
pode ser escrita como
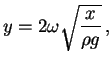
![$\displaystyle u_k(x, t) = J_0\left(z_{0, k} \sqrt{\frac{x}{L}}\right) \left[ A_...
..._k \sin \left( \frac{z_{0, k}}{2}\sqrt{\frac{\rho g}{L}} t \right) \right] \, ,$](img136.png)

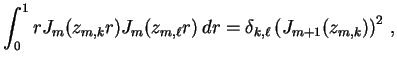
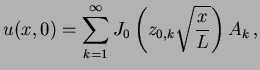
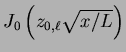 ,
integrando em
,
integrando em ![$\displaystyle \frac{\partial u}{\partial t}(x, t) = \sum_{k = 1}^{\infty} J_0\l...
...B_k \cos\left( \frac{z_{0, k}}{2}\sqrt{\frac{\rho g}{L}} t \right) \right] \, .$](img152.png)
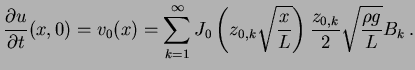
![$\displaystyle u(x, t) =
\frac{1}{2 L (J_1(z_{0, \ell}))^2}\int_0^L dx^\prime \l...
...) \cos\left( \frac{z_{0, k}}{2}\sqrt{\frac{\rho g}{L}} t \right)
\right] u_0(x)$](img157.png)
![$\displaystyle + \; \frac{1}{L \, z_{0,\ell} \, (J_1(z_{0, \ell}))^2}
\sqrt{\fra...
...sin \left( \frac{z_{0, k}}{2}\sqrt{\frac{\rho g}{L}} t \right)
\right] v_0(x) ,$](img158.png)